Hilbert's basis theorem
In mathematics, specifically commutative algebra, Hilbert's basis theorem states that every ideal in the ring of multivariate polynomials over a Noetherian ring is finitely generated. This can be translated into algebraic geometry as follows: every algebraic set over a field can be described as the set of common roots of finitely many polynomial equations. Hilbert (1890) proved the theorem (for the special case of polynomial rings over a field) in the course of his proof of finite generation of rings of invariants.
Hilbert produced an innovative proof by contradiction using mathematical induction; his method does not give an algorithm to produce the finitely many basis polynomials for a given ideal: it only shows that they must exist. One can determine basis polynomials using the method of Gröbner bases.
Contents |
Proof
The following more general statement will be proved.
Theorem. If 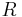 is a left- (respectively right-) Noetherian ring, then the polynomial ring
is a left- (respectively right-) Noetherian ring, then the polynomial ring ![R[X]\,](/2012-wikipedia_en_all_nopic_01_2012/I/0b038123bddb92ada15e643d5302f4df.png) is also a left- (respectively right-) Noetherian ring.
is also a left- (respectively right-) Noetherian ring.
It suffices to consider just the "Left" case.
Proof (Theorem)
Suppose per contra that ![\mathfrak{a}\subseteq R[X]\,](/2012-wikipedia_en_all_nopic_01_2012/I/9d7657186173d204b0b1d1196245c7be.png) were a non-finitely generated left-ideal. Then it would be that by recursion (using the axiom of countable choice) that a sequence
were a non-finitely generated left-ideal. Then it would be that by recursion (using the axiom of countable choice) that a sequence 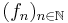 of polynomials could be found so that, letting
of polynomials could be found so that, letting 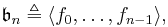
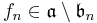 of minimal degree. It is clear that
of minimal degree. It is clear that 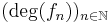 is a non-decreasing sequence of naturals. Now consider the left-ideal
is a non-decreasing sequence of naturals. Now consider the left-ideal 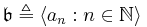 over
over 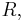 where the
where the 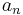 are the leading coefficients of the
are the leading coefficients of the 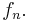 . Since
. Since 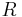 is left-Noetherian, we have that
is left-Noetherian, we have that 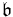 must be finitely generated; and since the
must be finitely generated; and since the 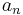 comprise an
comprise an 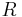 -basis, it follows that for a finite amount of them, say
-basis, it follows that for a finite amount of them, say 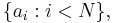 will suffice. So for example,
will suffice. So for example, 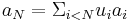 some
some 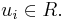 Now consider
Now consider 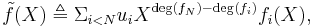 whose leading term is equal to that of
whose leading term is equal to that of 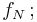 moreover
moreover 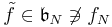 so
so 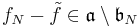 of degree
of degree 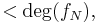 contradicting minimality.
contradicting minimality.
|
|
A constructive proof (not invoking the axiom of choice) also exists.
Proof (Theorem):
Let ![\mathfrak{a}\subseteq R[X]\,](/2012-wikipedia_en_all_nopic_01_2012/I/9d7657186173d204b0b1d1196245c7be.png) be a left-ideal. Let
be a left-ideal. Let 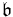 be the set of leading coefficients of members of
be the set of leading coefficients of members of 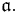 This is obviously a left-ideal over
This is obviously a left-ideal over 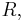 and so is finitely generated by the leading coefficients of finitely many members of
and so is finitely generated by the leading coefficients of finitely many members of 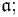 say
say 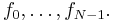 Let
Let 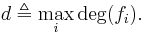 Let
Let 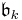 be the set of leading coefficients of members of
be the set of leading coefficients of members of 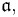 whose degree is
whose degree is 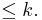 As before, the
As before, the 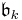 are left-ideals over
are left-ideals over 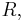 and so are finitely generated by the leading coefficients of finitely many members of
and so are finitely generated by the leading coefficients of finitely many members of 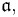 say
say 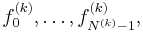 with degrees
with degrees 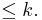 Now let
Now let ![\mathfrak{a}^{\ast}\subseteq R[X]\,](/2012-wikipedia_en_all_nopic_01_2012/I/92fef2afd76e0c4fc0ee8d6df0edfa04.png) be the left-ideal generated by
be the left-ideal generated by 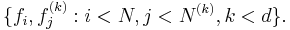 We have
We have 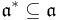 and claim also
and claim also 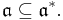
Suppose per contra this were not so. Then let 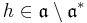 be of minimal degree, and denote its leading coefficient by
be of minimal degree, and denote its leading coefficient by 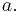
Case 1: 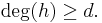 Regardless of this condition, we have
Regardless of this condition, we have 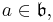 so is a left-linear combination
so is a left-linear combination 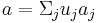 of the coefficients of the
of the coefficients of the 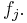 Consider
Consider 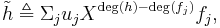 which has the same leading term as
which has the same leading term as 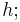 moreover
moreover 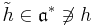 so
so 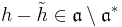 of degree
of degree 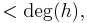 contradicting minimality.
contradicting minimality.
Case 2:  Then
Then  so is a left-linear combination
so is a left-linear combination 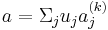 of the leading coefficients of the
of the leading coefficients of the 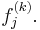 Considering
Considering 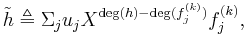 we yield a similar contradiction as in Case 1.
we yield a similar contradiction as in Case 1.
Thus our claim holds, and 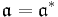 which is finitely generated.
which is finitely generated.
|
|
Note that the only reason we had to split into two cases was to ensure that the powers of 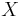 multiplying the factors, were non-negative in the constructions.
multiplying the factors, were non-negative in the constructions.
Applications
Let  be a Nötherian commutative ring. Hilbert's basis theorem has some immediate corollaries. First, by induction we see that
be a Nötherian commutative ring. Hilbert's basis theorem has some immediate corollaries. First, by induction we see that ![R[X_{0},X_{1},\ldots,X_{n-1}]\,](/2012-wikipedia_en_all_nopic_01_2012/I/7240d1e4b86dd923a85b502c0e07e4f4.png) will also be Nötherian. Second, since any affine variety over
will also be Nötherian. Second, since any affine variety over 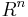 (i.e. a locus-set of a collection of polynomials) may be written as the locus of an ideal
(i.e. a locus-set of a collection of polynomials) may be written as the locus of an ideal ![\mathfrak{a}\subseteq R[X_{0},X_{1},\ldots,X_{n-1}]\,](/2012-wikipedia_en_all_nopic_01_2012/I/24ba4ef9228274429d707ebafa716925.png) and further as the locus of its generators, it follows that every affine variety is the locus of finitely many polynomials — i.e. the intersection of finitely many hypersurfaces. Finally, if
and further as the locus of its generators, it follows that every affine variety is the locus of finitely many polynomials — i.e. the intersection of finitely many hypersurfaces. Finally, if 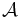 were a finitely-generated
were a finitely-generated 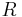 -algebra, then we know that
-algebra, then we know that ![\mathcal{A}\cong R[X_{0},X_{1},\ldots,X_{n-1}]/\langle\mathfrak{a}\rangle\,](/2012-wikipedia_en_all_nopic_01_2012/I/dc21c460337199890e123853b562b5db.png) (i.e. mod-ing out by relations), where
(i.e. mod-ing out by relations), where 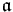 a set of polynomials. We can assume that
a set of polynomials. We can assume that 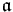 is an ideal and thus is finitely generated. So
is an ideal and thus is finitely generated. So 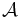 would be a free
would be a free 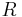 -algebra (on
-algebra (on 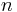 generators) generated by finitely many relations
generators) generated by finitely many relations ![\mathcal{A}\cong R[X_{0},X_{1},\ldots,X_{n-1}]/\langle p_{0},\ldots,p_{N-1}\rangle](/2012-wikipedia_en_all_nopic_01_2012/I/886d7a37ea64b2cfa85fbceffb8a0e1f.png) .
.
Mizar System
The Mizar project has completely formalized and automatically checked a proof of Hilbert's basis theorem in the HILBASIS file.
References
- Cox, Little, and O'Shea, Ideals, Varieties, and Algorithms, Springer-Verlag, 1997.
- Hilbert, David (1890), "Ueber die Theorie der algebraischen Formen", Mathematische Annalen 36 (4): 473–534, doi:10.1007/BF01208503, ISSN 0025-5831
 (Thm)
(Thm)